Из вершины А правильного треугольника ABC проведен к его плоскости перпендикуляр АМ....

Question

Из вершины А правильного треугольника ABC проведен к его плоскости перпендикуляр АМ. Точка М соединена с точками B и C. тангенс угла,образованного стороной МB с плоскостью треугольника ABC,равен 0,5. найдите двугранный угол, образованный плоскостями ABC и MBC

Answer 1

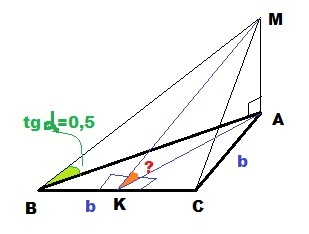
ΔABC :  AB = BC = AC = b
AM⊥(ΔABC) ⇒ ∠MAB = ∠MAC = 90°

ΔMAB :  ∠MAB = 90°; tg∠MBA = 0,5  ⇒
MA = AB*tg∠MBA = 0,5b

ΔABC : AK⊥BC  ⇒ AK = b*sin60° = b√3/2
AB=AC - проекции наклонных на плоскость равны ⇒ 
равны наклонные  MB = MC  ⇒
ΔBMC - равнобедренный  ⇒  MK⊥BC  ⇒
∠MKA равен двугранному углу между плоскостями  MBC и ABC.

ΔMKA : ∠MAK = 90°; MA = 0,5b;  AK = b√3/2  ⇒
tg∠MKA = MA / AK = 0,5b / (b√3/2) =   ⇒
∠MKA = 30°

Ответ: двугранный угол равен 30°

---