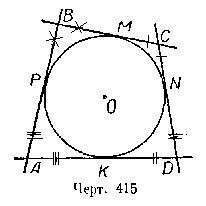
В описанном четырёхугольнике суммы противоположных сторон равны. Пусть четырёхугольник ABCD описан около окружности (черт. 415), т. е. стороны его АВ, ВС, CD и DA — касательные к этой окружности.
Требуется доказать, что АВ + CD =AD + ВС. Обозначим точки касания буквами М, N, К, Р, На основании свойств касательных, проведённых к окружности из одной точки, имеем:
АР = АК;
ВР = ВМ;
DN = DK;
CN = СМ.
Сложим почленно эти равенства. Получим:
АР + ВР + DN + CN = АК + ВМ +DK + СМ,
т. е. АВ + CD = AD + ВС, что и требовалось доказать.