Для получения вектора разности (c) = (a-b) начала векторов соединяются и началом вектора разности (c) будет конец вектора (b)
(вычитаемое), а концом - конец вектора (a) (уменьшаемое).
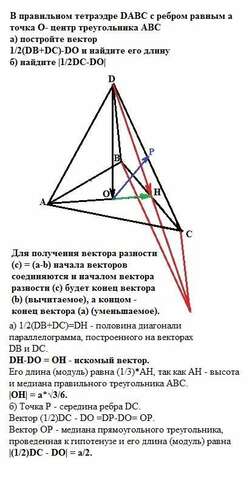
а) 1/2(DB+DC)=DH - половина диагонали параллелограмма, построенного на векторах DB и DC.
DH-DO = OH - искомый вектор.
Его длина (модуль) равна (1/3)*АН, так как АН - высота и медиана
правильного треугольника АВС.
|OH| = a*√3/6.
б) Точка Р - середина ребра DC.
Вектор (1/2)DC - DO =DP-DO= OP.
Вектор ОР - медиана прямоугольного треугольника, проведенная к
гипотенузе и его длина (модуль) равна
|(1/2)DC - DO| = а/2.