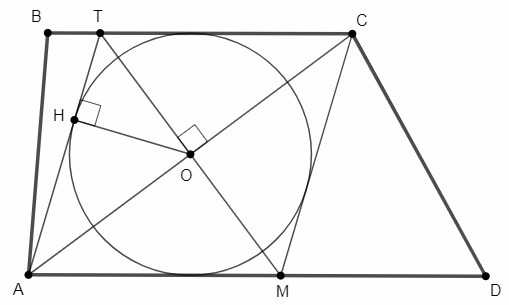
AO=CO, ∠AOM=∠COT=90°
∠MAO=∠TCO (нактерст лежащие при параллельных основаниях трапеции)
△AOM=△COT (по стороне и прилежащим к ней углам)
OM=OT
Диагонали ATCM перпендикулярны и точкой пересечения делятся пополам, ATCM - ромб.
В ромб можно вписать окружность (так как суммы его противоположных сторон равны). Центр вписанной окружности ромба - точка пересечения диагоналей (так как диагонали являются биссектрисами его углов). Радиус вписанной окружности - перпендикуляр из центра на сторону (OH⊥AT).
AO=AC/2=16/2=8
△AOT - египетский треугольник (3:4:5), множитель 2:
OT=3*2=6 (AO=4*2; AT=5*2)
Высота из прямого угла делит треугольник на подобные друг другу и исходному.
△OHT~△AOT, k=OT/AT=0,6
OH=AO*k =8*0,6 =4,8
------------------------------------------------------------------------------------------------------------
Диагонали четырехугольника точкой пересечения делятся пополам - признак параллелограмма. Диагонали параллелограмма перпендикулярны - признак ромба.