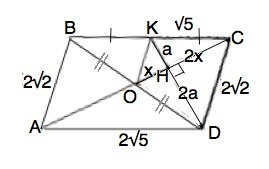
ABCD- параллелограмм. Диагонали параллелограмма при пересечении делятся пополам.
В треугольнике ВСD
ВО=OD=> CO - медиана треугольника ВСD.
BK=CK( дано)=>
DK- медиана ∆BCD.
Н- точка пересечения медиан, угол CHD=90°( дано)
Медианы треугольника точкой их пересечения делятся в отношении 2:1, считая от вершины.
Примем КН=а, тогда DH=2a
Примем ОН=х, тогда СН=2х
––––––––––––––
Из прямоугольного ∆ КСН по т.Пифагора
СН²=КC²-КH²
4х²=(√5)²-a²
Из прямоугольного ∆ СDH по т.Пифагора
СН²=CD²-DH²
4x²=8-4a²
Приравняем значения 4х* из двух уравнений:
8-4a²=(√5)²-a²
3a²=8-5
a²=1⇒
a=1
Подставим это значение в уравнение
4х²+4а²=8 ⇒
х²+1²=2
х=1
Из прямоугольного ∆ ОНD по т.Пифагора
ОD²=OH²+DH²=1+4=5
OD=√5
BD=2√5 (ед. длины)