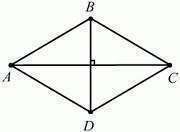
1)Т.к. ромб является параллелограммом, то сумма углов прилежащих к стороне ромба равна 180 град., т.е. L A+ L B =180
L A = 180- L B = 180-120=60.
2) Построим диагональ ВD. ВD- биссектриса угла В ( св-во ромба),
тогда L CBD = L CDB =120/2=60.
Таким образом тр-к СВD-равносторонний , т.е. BD =ВС= a (! длина стороны ромба).
3) Из тр-ка ВСО- прям.: L ВСО = 60/2=30 град., тогда
СО =ВО* корень из 3 = а*корень из 3 ,значит
АС =2* СО=2* а*корень из 3 (! св-во пар-ма: диагонали точкой пересечения...).
Ответ: 2* а*корень из 3; а.