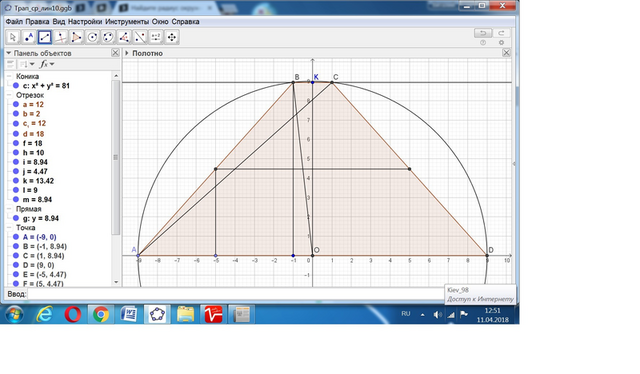
Дано: площадь трапеции S = 40√5,
средняя линия L = 10.
радиус описанной окружности R = ?.
Обозначим половину верхнего основания трапеции за х.
Нижнее основание равно 2R.
Высота трапеции h = S/L = 40√5/10 = 4√5.
По условию задания (2R + 2x)/2 = 10 или R + x = 10.
Отсюда R = 10 - x.
С другой стороны радиус по Пифагору равен:
R = √(х² + h²) = √(х² + (4√5)²) = √(х² + 80).
Приравняем: 10 - x = √(х² + 80).
Возведём в квадрат: 100 - 20х + х² = х² + 80.
Получаем 20х = 100 - 80 = 20.
Отсюда х = 20/20 = 1.
Получаем ответ: R = 10 - 1 = 9.