Нить, намотанную ** ось катушки, тянут со скоростью u под углом α к горизонту. Катушка...

Question

132 просмотров

Нить, намотанную на ось катушки, тянут со скоростью u под углом α к горизонту. Катушка катится по горизонтальной плоскости без проскальзывания. Найти скорость поступательного движения оси катушки и ее угловую скорость вращения. Определить скорость и ускорение точки А. Радиус внутренней части катушки - r , внешней - R .

Определить под каким углом катушка будет стоять на месте, под какими углами начнёт двигаться влево или вправо.

Решение нужно дать с подробным пояснением используемых формул и законов.

Физика kvintovskiy_zn (1.2k баллов) 31 Май, 18 | 132 просмотров

Дан 1 ответ

Правильный ответ

1) Условие отсутствия проскальзывания: если катушка поворачивается на угол $\alpha$ , то она продвигается на $\alpha R$ . В терминах скоростей: если круговая скорость вращения относительно центра $\omega$ , то скорость поступательного движения $v=\omega R$ .

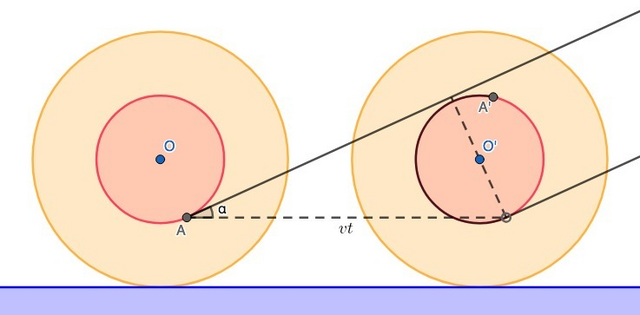
Рассмотрим два положения катушки, между которыми прошло короткое время t. За это время её центр успевает продвинуться от точки O до точки O' на $vt=\omega R t$ , сама она проворачивается на угол $\omega t$ .

Вычислим, на какую величину изменилась длина свободной части нити. Во-первых, часть нити намоталась на катушку (изменение длины пропорционально углу, на который провернулась катушка, вклад равен длине дуги AA' $-\omega t\cdot r$ ), во-вторых, часть нити освободилась при поступательном движении (вклад равен длине катета в выделенном треугольнике $vt\cos\alpha$ ). Суммарное изменение по условию должно равняться ut:
$vt\cos\alpha-\omega tr=ut\\ \omega(R\cos\alpha-r)=u\\ \boxed{\omega=\dfrac{u}{R\cos\alpha-r}}\\\boxed{v=\omega R=\dfrac {uR}{R\cos\alpha-r}}$

Если v > 0 (т.е. $R\cos\alpha\ \textgreater \ r$ ), катушка движется вправо, если v < 0 ( $R\cos\alpha\ \textless \ r$ ) – влево.
Если $R\cos\alpha=r$ , то движения в плоскости не будет.

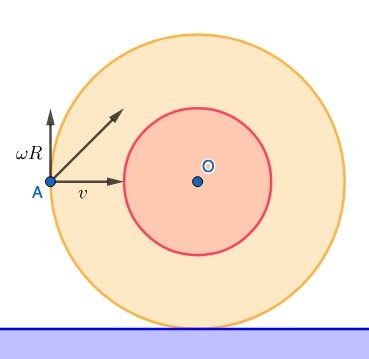
2) Скорость и ускорение точки А (рис. 2)
Скорость точки A равна сумме скорости, связанной с вращением относительно центра, которая равна $\omega R$ и направлена по касательной, и скорости поступательного движения v. В данном случае $v=\omega R$ , скорости направлены перпендикулярно друг другу, значит, по правилу сложения векторов полная скорость направлена так, как изображено на рисунке, и её модуль равен $v\sqrt 2$ .

Поступательное движение равномерное, поэтому ускорение возникает только из-за вращения, оно направлено по направлению к центру тела и равно $\omega^2 R$ .

nelle987_zn (148k баллов) 31 Май, 18