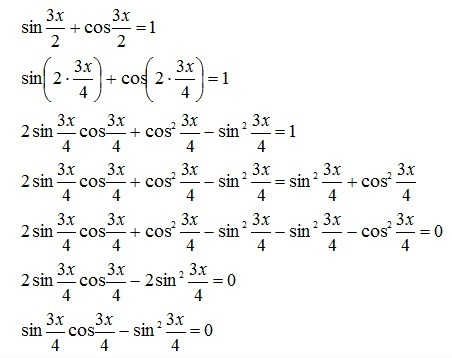Здесь можно решить уравнение, если расписать и синус и косинус через двойной угол, т.е. представить 3x/2=2*3x/4. Тогда имеем синус и косинус двойного угла, которые можно расписать по формулам:
sin(2*3x/4)=2*sin(3x/4)*cos(3x/4)
cos(2*3x/4)=cos²(3x/4)-sin²(3x/4)
Тогда получим: 2*sin(3x/4)*cos(3x/4)+cos²(3x/4)-sin²(3x/4)=1
Правую часть равенства можно расписать как тригонометрическое тождество: sin²x+cos²x=1.
Для нашего примера получим: sin²(3x/4)+cos²(3x/4)=1
Итак, имеем:
2*sin(3x/4)*cos(3x/4)+cos²(3x/4)-sin²(3x/4)=sin²(3x/4)+cos²(3x/4)
А далее переносим влево все слагаемые и упрощаем выражение:
2*sin(3x/4)*cos(3x/4)+cos²(3x/4)-sin²(3x/4)-sin²(3x/4)-cos²(3x/4)=0
Тут сокращаются квадраты косинусов, а после приведения подобных получим:
2*sin(3x/4)*cos(3x/4)-2*sin²(3x/4)=0
Вынесем за скобку общий множитель 2:
2*(sin(3x/4)*cos(3x/4)-sin²(3x/4))=0
Сократим обе части равенства на 2:
sin(3x/4)*cos(3x/4)-sin²(3x/4)=0
А далее применяем способ приведения к единственной функции: разделим обе части равенства на ту функцию, которая имеет самую большую степень (здесь это sin²(3x/4)). Помним, что cosx/sinx=ctgx, и получим:
(sin(3x/4)*cos(3x/4))/sin²(3x/4)-sin²(3x/4)/sin²(3x/4)=0
В первом слагаемом сократим дробь на sin(3x/4), а вторая дробь будет равна 1, т.к. синусы полностью сокращаются.
cos(3x/4)/sin(3x/4)-1=0
ctg(3x/4)-1=0
ctg(3x/4)=1
Котангенс равен 1, если угол равен π/4 с периодом πκ, κ∈Z
При этом нужно помнить, что мы делили уравнение на sin²(3x/4), т.е. эта функция не должна равняться 0 (т.к. делить на 0 нельзя).
С учетом этого ограничения, окончание решения и ответ приведены на рисунках