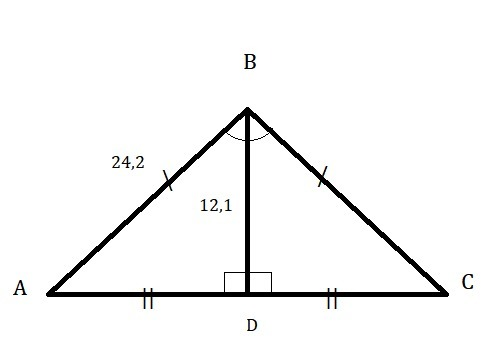
По условию Δ АВС - равнобедренный.
По свойствам равнобедренного треугольника:
1)Боковые стороны равны:
АВ=ВС = 24,2 см
2) Углы при основании равны:
∠А = ∠ С
3) Высота к основанию является биссектрисой и медианой:
BD = 12,1 см - высота к основанию АС
∠BDA=∠BDC = 90°
AD= DC
∠AВD = ∠CBD
ΔВDA = ΔBDC - прямоугольные и равные треугольники
Катеты : ВD = 12,1 см , AD = DC
Гипотенуза : AB=ВС= 24,2 см
BD/AB = ВD/ВC = 12,1/24,2 = 1/2 ⇒ BD =¹/₂* АВ = ¹/₂ *ВС
Катет , лежащий против угла в 30°, равен половине гипотенузы.
Следовательно:
∠A = ∠С = 30°
Сумма углов любого треугольника = 180°.
∠В = 180 - 2*30 = 180 - 60 = 120°
Ответ : ∠А = ∠С = 30° ; ∠В = 120° .