1) надо найти площадь основания, для этого надо знать его радиус r
Его определить можно через длину окружности основания, которая равна длине дуги развертки боковой поверхности, она неизвестна-но ее можно найти через радиус R развертки(в конусе это будет образующая)
Площадь боковой поверхности S(бок)=piR^2/360*36=piR^2/10=10
piR^2=100
R^2=100/pi
R=10/√pi
L=2piR/360*60=2piR/10=piR/5=pi*10/(√pi*5)=2√pi-длина окружности основания
2pir=2√pi
r=1/√pi
S(основания)=pir^2=1
Тогда полная поверхность конуса S=S(осн)+S(бок)=1+10=11
2)при вращении треугольника вокруг катета получится конус с радиусом и высотой а
S=pia^2+pia*a√2=pia^2(1+√2)
2a)при вращении вокруг гипотенузы образуется поверхность из двух одинаковых конусных боковых поверхностях с образующими, равными а и радиусом a/√2
S=2S(б)=2*pi*a*a/√2=pia^2√2
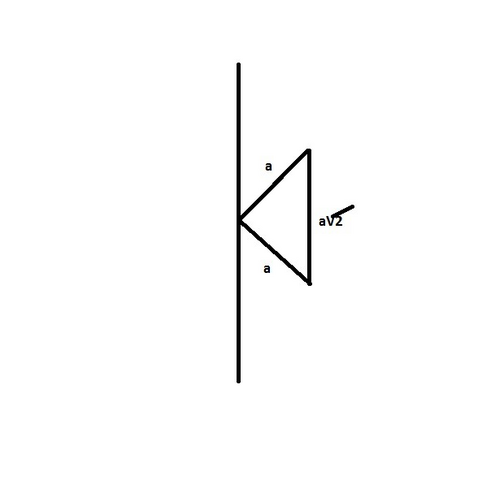
2в) на рисунке фигура вращения, она состоит из двух частей
ломаная из 2 катетов образует поверхность, равную найденной в предыдущем задании pia^2√2 и осталось найти площадь , образованную вращением гипотенузы-это будет боковая поверхность цилиндра с высотой a√2 и радиусом a/√2
S1=2pi*a/√2*a√2=2pia^2
тогда вся поверхность вращения будет S=2pia^2+pia^2√2=pia^2(2+√2)