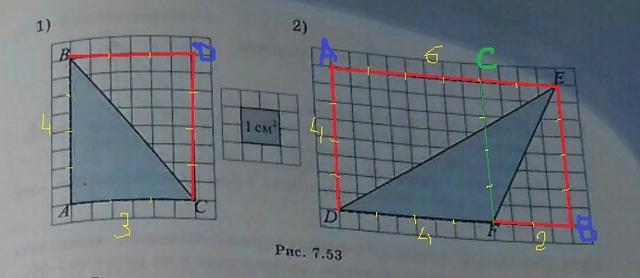
1) Дополним треугольник АВС до прямоугольника АВСD(проведем через точку В прямую, параллельную АС и отложим на прямой отрезок ВD, и построим аналогично отрезок СD).
Треугольник АВС занимает половину прямоугольника ABCD.
Длина прямоугольника 4 см, ширина 3 см.
S(ABC) = (1/2)*S(ABCD) = (1/2)*(3*4) = (1/2)*12 = 6 (см²).
Ответ: 6 см²
2) Дополним ΔDEF до прямоугольника DАЕВ. Длина прямоугольника 6 см, ширина 4 см.
Наш ΔDEF занимает вместе с ΔFEB половину площади.прямоугольника DAEF.
Чтобы найти площадь ΔFEB достроим его до прямоугольника CEBF, c длиной 4 см и шириной 2 см. Площадь ΔFEB составляет половину площади CEBF.
S(DEF) = (1/2)*S(DAED) - (1/2)*S(CEBF) = (1/2)*(6*4) - (1/2)*(2*4) = (1/2)*24 - (1/2)*8 = 12 - 4 = 8(см²)
Ответ:8 см²