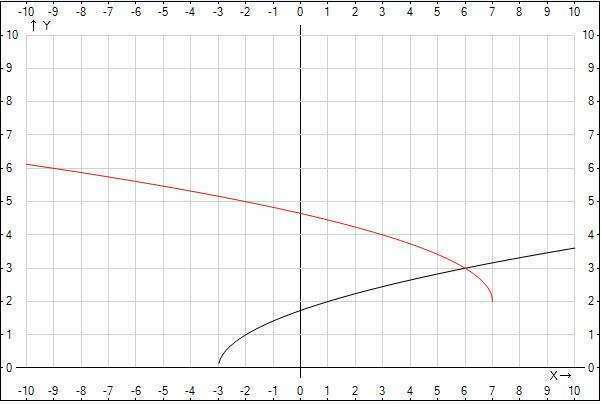
Sqrt(x+3) = 2 + sqrt(7-x) - возведем обе части уравнения в квадрат
x+3>=0, 7-x>=0; -3<=x<=7<br>x+3 = 4 + 4*sqrt(7-x) + 7 - x
2x - 8 = 4*sqrt(7-x) - еще раз возведем в квадрат обе части
4x^2 - 32x + 64 = 16*(7 - x)
4x^2 - 32x + 64 - 112 + 16x = 0
4x^2 - 16x - 48 = 0
x^2 - 4x - 12 = 0, D = 16 + 4*12 = 16 + 48 = 64
x1 = (4 - 8)/2 = -2
x2 = (4 + 8)/2 = 6
Проверка: sqrt(-2+3) - sqrt(7+2) =1 - 3 = -2 # 2 - (x = -2 не является корнем)
sqrt(6+3) - sqrt(7-6) =3 - 1 = 2 - верно, корень.
Ответ: x = 6
P.S. Также четко видно решение на графике.