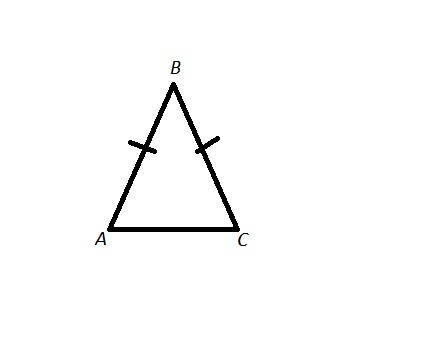
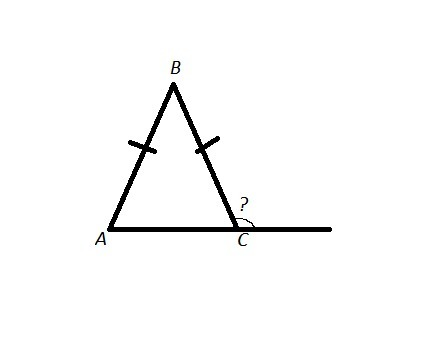Т.к. AB = BC ⇒ ΔABC - равнобедренный
У равнобедренного Δ-ка углы при основании равны ⇒ ∠A + ∠C = x + x = 2x
Сумма всех углов Δ-ка равна 180° ⇒ ∠A + ∠B + ∠ C = 180°
Решаем уравнение:
x + x + 110° = 180°
2x = 180° - 110°
2x = 70°
x = 35°
Дорисовываем линию около ∠C
Получаем развернутый угол, равный 180°
Для того, чтобы узнать внешний угол, от 180° - ∠C = 180° - 35 = 145°
Ответ: Внешний угол при вершине C, равен 145°