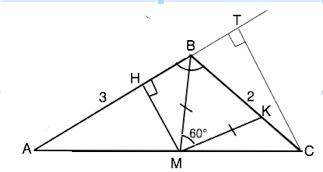
На рисунке треугольник ВМК равнобедренный, угол ВМК=60°, поэтому углы при его основании ВК также равны 60°.
Указано равенство ∠АВМ и ∠СВМ.
Следовательно, ВМ биссектриса, ∠НВМ=60°, ⇒ ∠АВС=120°
Проведем высоту СТ к стороне АВ.
Высота из вершины острого угла тупоугольного треугольника находится вне треугольника и пересекает продолжение стороны.
∆ СВТ прямоугольный с углом СВТ=60° ( смежный углу АВС).
ТС=ВС•sin60°=2:√3/2=√3
Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон =>
АМ:МС=АВ:ВС=3/2
АС=АМ+МС= 3+2=5 частей.
Проведем МН║СТ
Прямоугольные ∆ АТС и АНМ подобны по общему острому углу А.
k=АМ:АС=3/5
НМ=ТС•3/5=(√3)•3/5
BM=HM:sin60°=6/5=1,2 (ед. длины)
–––––––––––––
Есть формулы для нахождения биссектрисы произвольного треугольника. Для данной задачи подойдет формула
, где L - биссектриса, а и b- стороны треугольника, α - угол между ними. Вычисления дают длину ВМ=1,2
