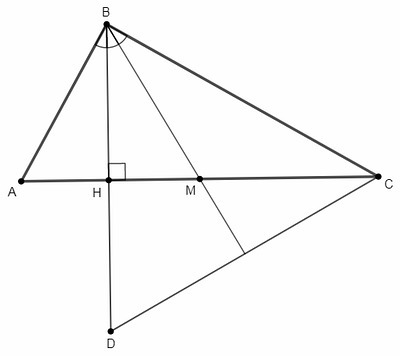
BM - медиана, AM=CM. BH - высота и биссектриса в △ABM, следовательно и медиана, HM=AM/2=CM/2. Точка М делит CH в отношении 2:1, считая от вершины С.
D∈BH, BH=HD
CH - медиана в △BCD, M - точка пересечения медиан △BCD (по основному свойству). CH - медиана и высота, BM - медиана и биссектриса, следовательно △BCD - равносторонний, ∠DBC=60°.
∠ABC= 3/2 *∠DBC =90°