Если радиус 3, то OB=3√2 (диагональ квадрата со стороной 3).
Исправим условие: AO=√10 см
-----------------------------------------------------------------------------------------------------------------
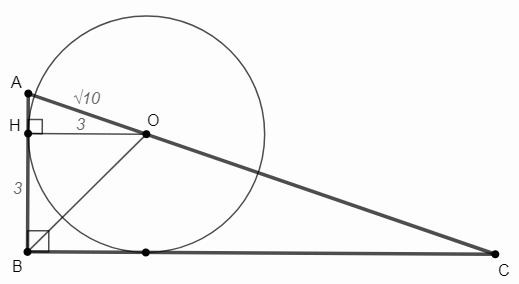
Окружность касается AB в точке H
OH=3 см, ∠AHO=90° (касательная перпендикулярна радиусу, проведенному в точку касания)
AH=√(AO^2-OH^2) =√(10-9) =1 (см)
Центр окружности, вписанной в угол, лежит на биссектрисе угла.
△BHO - равнобедренный (прямоугольный с углом 45°), BH=ОН=3 (см)
AB=AH+BH =4 (см)
△ABC~△AHO (по двум углам, прямоугольные, ∠A - общий)
BC=OH*AB/AH =3*4=12 (см)
S(ABC)=AB*BC/2 =4*12/2=24 (см^2)