Дан куб ABCDA1B1C1D1 с ребром . Найдите расстояние между прямыми AA1 и D1K, где точка K...

Question

Дан куб ABCDA1B1C1D1 с ребром . Найдите расстояние между прямыми AA1 и D1K, где точка K - середина ребра BC

Answer 1

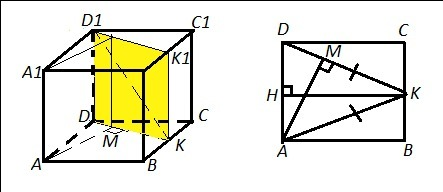
АА1 и D1K - cкрещивающиеся прямые.
D1K - лежит в пл. DD1K1K.  
Расстоянием от АА1 до D1K будет расстояние от АА1 до DD1K1K , т.к. АА1 параллельна плоскости DD1K1K ( прямая АА1 параллельна прямой DD1, лежащей в пл. DD1K1K ⇒ AA1║DD1K1K). А это расстояние = расстоянию от т. А до пл. DD1K1K . Проведём АМ⊥DD1K1K ( AM⊥DK  и АМ⊥DD1).
АМ - искомое расстояние.
АМ - высота равнобедренного ΔАKD ( KD=AK, т.к. СК=КВ и АВ=DC ).
АK=DK=√(AB²+BK²)=√((2√5)²+(√5)²)=√(20+5)=5.
KH⊥AD  ⇒  KH=DC=AB=2√5 ( т.к. АВСD - квадрат)
S(ΔAKD)=1/2*AD*KH=1/2*2√5*2√5=2*5=10
S(ΔAKD)=1/2*DK*AM=1/2*5*AM  ⇒  5/2*AM=10  ⇒  AM=10:(5/2)=4

---

Comments

Спрашивали расстояние между прямыми, а не расстояние до плоскости DKK1D1 или DK.

---

Расстояие между этими прямыми = расстоянию от АА1 до плоскости, параллельной АА1 и содержащей D1K.

---

Если есть возможность, то на рисунке добавить отрезок - расстояние.

---

На рис. - это АМ

---

Надо до прямой D1K, а не DK. Начертить правильно, а потом доказывать, что проекция будет равна АМ.

---

Расст. между скрещ. прямыми = расстоянию между одной из прямых (АА1) и плоскостью, параллельной АА1, содержащей D1K. Расстояние от прямой до параллельной ей плоскости = расстоянию от любой точки этой прямой (т.А) до плоскости DD1K1K. Что вы хотите ещё добавлять? Я всё нарисовала.

---

Ладно, ладно.