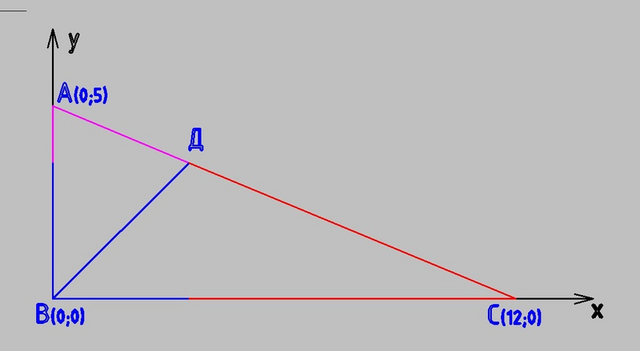
НАчало координат в прямом углу треугольника, y вверх, x вправо
B(0;0)
A(0;5)
C(12;0)
Уравнение прямой по двум точкам c координатами (x₁;y₁) (x₂;y₂)
(x - x₁)/(x₂ - x₁) = (y - y₁)/(y₂ - y₁)
Уравнение прямой АС
(x - 0)/(12 - 0) = (y - 5)/(0 - 5)
x/12 = -y/5 + 1
y/5 = 1 - x/12
y = 5 - 5x/12
Уравнение биссектрисы ВД
y = x
Находим точку пересечения Д
x = 5 - 5x/12
x + 5x/12 = 5
17x/12 = 5
x = 60/17
y = 60/17
Д(60/17; 60/17)
---
BA = A - B = A = (0;5)
AD = D - A = (60/17; 60/17) - (0;5) = (60/17; (60-5*17)/17) = (60/17; (60-85)/17) = (60/17; -25/17)
BA·AD = (0;5)·(60/17; -25/17) = 0*60/17 + 5*(-25/17) = -125/17