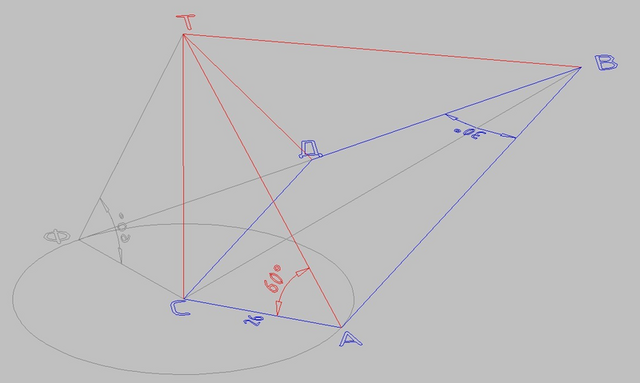
Трапеция в основании прямоугольная.
Её высота, она же боковая сторона, АС = 26 см
Грань АВТ наклонена к основанию на 60°, значит
∠САТ = 60°
в ΔСАТ
∠СТА = 90 - 60 = 30°
Катет против угла в 30° в два раза меньше гипотенузы,
АТ = 2*26 = 52 см
Высота пирамиды по теореме Пифагора
СТ = √(АТ² - АС²) = √(52² - 26²) = 26√3 см
S(CTA) = 1/2*СТ*СА = 1/2*26*26√3 = 338√3 см²
---
Плоскость ТДВ наклонена к плоскости основания по условию на 60°
Линия ДВ является линией пересечения плоскостей
∠СФТ является углом между плоскостями
∠СФТ = 60°
ФС = 26 см
---
в ΔСДФ
∠СДФ = 30°
∠СФД = 90°
СД = 2*ФС = 52 см
S(СДТ) = 1/2*СТ*СД = 1/2*26√3*52 = 676√3 см²
---
в ΔАВС
∠АВС = 15°
tg(15°) = 2-√3
ctg(15°) = 2+√3
АВ/АС = ctg(15°)
АВ = 26*(2+√3) см
АТ = 52 см
S(АВТ) = 1/2*АВ*АТ = 1/2*26*(2+√3)*52 = 1352 + 676√3 см²
---
S(ДВТ) = S(ФВТ) - S(ФДТ) = S(АВТ) - S(ФДТ)
S(ФДТ) = 1/2*ФД*ФТ = 1/2*26√3*52 = 676√3 см²
S(ДВТ) = 1352 + 676√3 - 676√3 = 1352 см²
---
S(бок) = S(CTA) + S(СДТ) + S(АВТ) + S(ДВТ)
S(бок) = 338√3 + 676√3 + 1352 + 676√3 + 1352 = 2704 + 1690√3 см²