X^2 + |x^2 - 2x| = y^2 + |y^2 - 2y|
x^2 + |x(x-2)| = y^2 + |y(y-2)|
Нули модулей: х = 0, х = 2, у = 0, у = 2.
Построим график этой функции, для этого рассмотрим все 9 случаев (самое интересное происходит в случаях 6 и 8):
1) x >= 2, y >= 2:
Раскроем модули на этом участке, получим:
2x^2 - 2x = 2y^2 - 2y
x(x-1) = y(y-1)
График функции вида x^2 = y^2 - это крест, осталось только найти центр этого креста.
Центром будет точка, в которой одному значению х отвечает только одно значение у.
Т. е. x = -(x-1) => x = 0.5.
Тогда y(y-1) = -0.25 => y = 0.5.
2) x >= 2, 0 <= y < 2:<br>x^2 + x^2 - 2x = y^2 - y^2 + 2y
2x^2 - 2x = 2y
y = x^2 - x = x(x - 1)
При условии x >= 2, 0 <= y < 2 решений нет.<br>
3) x >= 2, y < 0
x^2 + x^2 - 2x = y^2 + y^2 - 2y
Аналогично случаю 1.
4) 0 <= x < 2, y >= 2:
Решений нет.
5) 0 <= x < 2, 0 <= y < 2:<br>x^2 - x^2 + 2x = y^2 - y^2 + 2y
х = у
График функции - прямая.
!6) 0 <= x < 2, y < 0:<br>
x^2 - x^2 + 2x = y^2 + y^2 - 2y
2x = 2y^2 - 2y
x = y*y - y = y(y - 1)
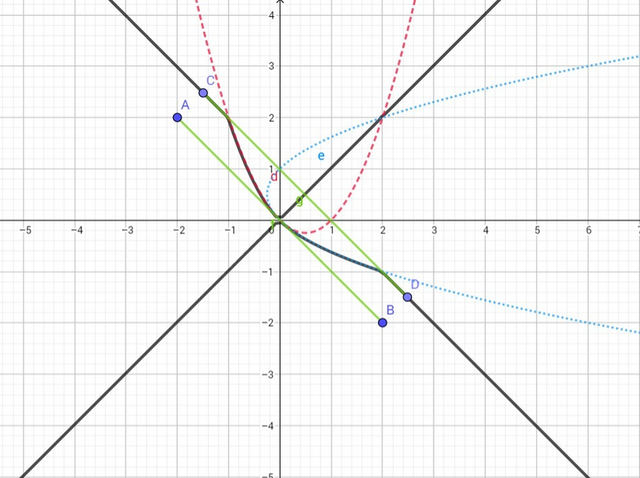
График этой функции (голубая линия) - парабола типа y = x(x-1), повернутая на 90 градусов по часовой стрелке вокруг оси в точке (0.5, 0.5).
7) x < 0, y >= 2:
2x^2 - 2x = 2y^2 - 2y
Аналогично случаю 1.
!8) x < 0, 0 <= y < 2:<br>
x^2 + x^2 - 2x = y^2 - y^2 + 2y
y = x(x-1)
График этой функции - парабола (розовая линия).
9) x < 0, y < 0:
2x^2 - 2x = 2y^2 - 2y
Аналогично случаю 1.
Используя эту информацию, строим график.
Видим, что 3 и более пересечения с прямой y = -x + a, график которой - прямая, проходящая из II четверти в IV (зеленые линии), будет в случае, если a E (0; -1].
Ответ: a E (0; -1].