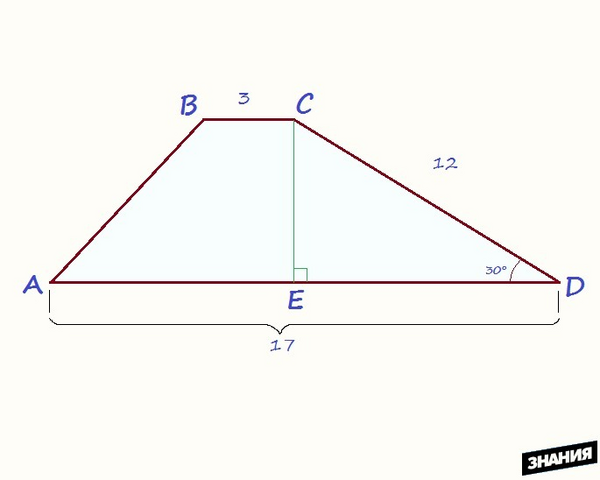
Дано:
ABCD
— трапеция.
BC = 3, AD = 17.
EC
— высота.
∠D = 30°
Найти:
S
— ?
Решение:
1) Рассмотрим трапецию ABCD.
Проведём высоту EC.
2) Рассмотрим ΔEDC.
Согласно свойству треугольника, катет, лежащий против угла в 30°, равен половине гипотенузы. Значит, EC = 1/2 CD.

3) Площадь трапеции равна полусумме оснований, умноженной на высоту:

Площадь трапеции равна 60 квадратных единиц.
В условии задачи единицы измерения (площади) нам не даны, поэтому в ответ запишем только число, без указания квадратных единиц.
Ответ: 60