Вариант I
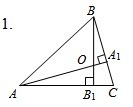
Дано: CAB = 42°.
Найти: ACO.
2. В треугольнике MNK биссектрисы пересекаются в точке О. Расстояние от точки О до стороны MN = 6 см, NK = 10 см. Найдите площадь треугольника NOK.
Вариант II
Найти: расстояние от точки О до стороны АС.
2. В треугольнике MNK медианы МР и NE пересекаются в точке О
и равны 12 и 15 см соответственно. Найдите площадь треугольника МОЕ, если МР NE