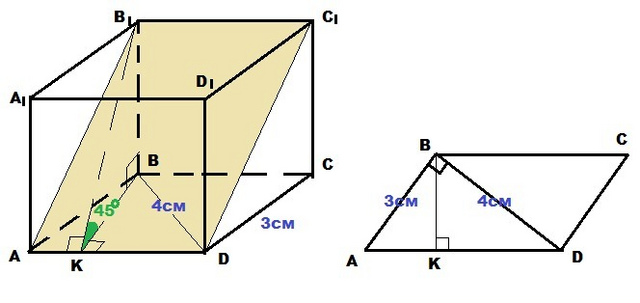
В основании прямого параллелепипеда лежит параллелограмм ABCD:
AB=3 см, BD=4 см; BD⊥AB ⇒
ΔABD - прямоугольный: ∠ABD = 90° ⇒
гипотенуза AD = 5 см (Пифагорова тройка 3,4,5)
 см
см
Площадь основания ( параллелограмма)
S₀ = AD*BK = 5*2,4 = 12 см²
Плоскость AB₁C₁ пересекает грань CC₁D₁D по линии DС₁║AB₁
BK⊥AD; BB₁⊥(ABCD) ( так как параллелепипед прямой) ⇒
B₁K⊥AD (по теореме о трёх перпендикулярах) ⇒
∠B₁KB - угол между плоскостью AB₁C₁D и плоскостью основания ABCD
⇒ ∠B₁KB = 45°
ΔKBB₁ - прямоугольный: ∠KBB₁ = 90°; ∠B₁KB = 45° ⇒
∠KB₁B = 45° и BB₁ = BK = 2,4 см
Площадь боковой поверхности параллелепипеда
S₁ = (AB + BC + CD + AD) * BB₁ = 16 * 2,4 = 38,4 см²
Площадь полной поверхности параллелепипеда
S = 2S₀ + S₁ = 2*12 + 38,4 = 62,4 см²
Ответ: S = 62,4 см²