Из точки К не лежащей ** окружности проведены 2 касательные КА и КВ к окружности с...

Question

Из точки К не лежащей на окружности проведены 2 касательные КА и КВ к окружности с центром в точке О. Найти угол АКВ , если угол АВО = 50 градусов. Сделайте рисунок пж , скиньте решение , даю 60 баллов

Answer 1

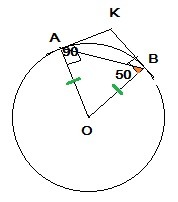
АО=ОВ как радиусы⇒ΔАОВ-равнобедренный, тогда ∠АОВ=180-(∠ОАВ+∠ОВА)=180-100=80°.
∠ОАК=∠ОВК=90° -касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
Зная, что сумма углов выпуклого четырехугольника равна 360°, найдем 
∠ АКВ=360-∠АОВ-2*90=100°.

---