Составьте уравнение касательной к графику функции y=x-1/x^2 параллельно прямой y=3x

Question

Дан 1 ответ

Maksim2009rus_zn · Answer 1 · 2018-05-31T16:26:56+0000

Уравнение касательной к графику функции $y=x-\cfrac{1}{x^2}$ параллельно прямой $y=3\,x$ будет выглядеть следующим образом: $y=ax+b$ , где a - коэффициент наклона касательной, он равен по условию 3, так как прямая параллельна прямой $y = 3x$ .
Таким образом, остается найти только коэффициент b.
Так как производная функции в точке $x_0$ равна углу наклона касательной данной функции в этой точке, то, приравняв производную к данному коэффициенту наклона (k = 3), найдем точку касания.

Производная функции равна: $y'=1 + \cfrac{2}{x^3}$ . Приравняем её к 3 и получим: $1 + \cfrac{2}{x^3} = 3; \\\\ \cfrac{2}{x^3}=2; \\\\ x^3 = 1 \Rightarrow x = 1$ .
Получим, что x = 1 - точка касания. Найдем значение функции в этой точке. $y(1)=1-\cfrac{1}{1^2}=0$ .
Значит, точка касания -- (1, 0).
Подставим эту точку в уравнение касательной и получим:
$y = 3x + b \, \Rightarrow \, 0 = 3\cdot1 + b \, \Rightarrow \, b = -3$ .

Получили уравнение касательной: $y=3x-3$

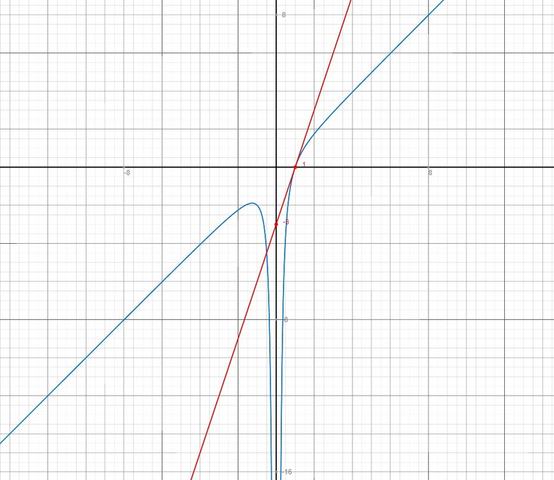
Проиллюстрируем исходную функцию и уравнение касательной на одном графике (см. вложения).