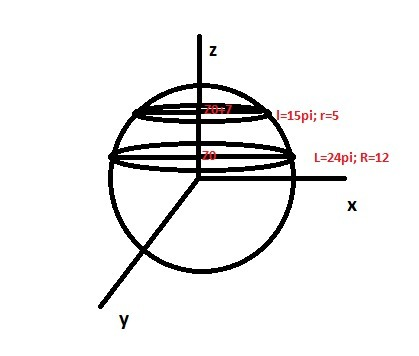
Вообщем я немного упростила это решение
Пусть большее сечение лежит выше центра шара по оси Z ,
его радиус 12 и центр в точке (0;0;z0)
Тогда его уравнение будет x^2+y^2+z0^2=R^2
Здесь R радиус сферы. Так как радиус большего сечения 12(24pi/2pi), то уравнение большего круга
Будет 12^2+z0^2=R^2
Меньшее сечение x^2+y^2+(z0+7)^2==R^2; 25+z0^2+14z0+47=R^2
Вычитаю из первого второе , получу
119-17z0-49=0
-14z0=-70
Z0=5
Выходит большее сечение находится от центра шара по оси z на
расстоянии 5, значит
R^2=5^2+12^2=169
R=13
S(cф)=4pi*13^2=676pi