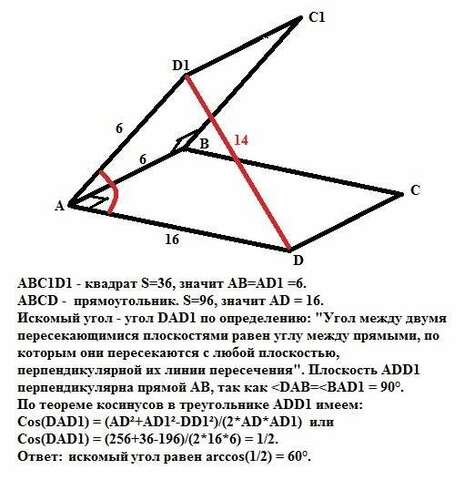
1. ABC1D1 - квадрат S=36, значит АВ=АD1 =6.
ABCD - прямоугольник. S=96, значит AD = 16.
Искомый угол - угол DAD1 по определению: "Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения". Плоскость ADD1 перпендикулярна прямой АВ, так как По теореме косинусов в треугольнике ADD1 имеем:
Cos(DAD1) = (AD²+AD1²-DD1²)/(2*AD*AD1) или
Cos(DAD1) = (256+36-196)/(2*16*6) = 1/2.
Ответ: искомый угол равен arccos(1/2) = 60°.
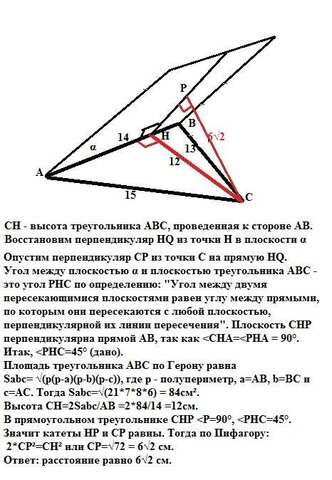
2. СН - высота треугольника АВС, проведенная к стороне АВ.
Восстановим перпендикуляр НQ из точки Н в плоскости α.
Опустим перпендикуляр СР из точки С на прямую НQ.
Угол между плоскостью α и плоскостью треугольника АВС - это угол РНС по определению: "Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения". Плоскость СНР перпендикулярна прямой АВ, так как <СНА=<РНА = 90°. Итак, <PHC=45° (дано).<br>Площадь треугольника АВС по Герону равна
Sabc= √(p(p-a)(p-b)(p-c)), где р - полупериметр, а=АВ, b=BC и c=AC. Тогда Sabc=√(21*7*8*6) = 84см².
Высота СН=2Sabc/AB =2*84/14 =12см.
В прямоугольном треугольнике СНР
2*СР²=СН² или СР=√72 = 6√2 см.
Ответ: расстояние равно 6√2 см.