Сумма острых углов прямоугольного треугольника равна 90°.
∠A=2x, ∠B=3x
∠A+∠B =90° <=> 2x +3x =90° <=> x= 90°/5 =18°
∠B=3x =18°*3 =54°
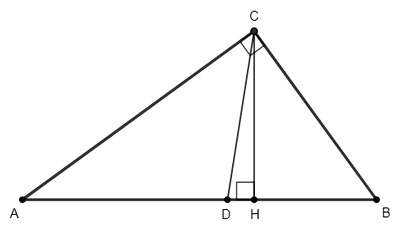
CH - высота, CD - биссектриса.
∠ACH= 90°-∠A =∠B =54°
∠ACD= ∠C/2 =45°
∠DCH= ∠ACH-∠ACD =54°-45° =9°
--------------------------------------
Высота CH делит делит угол C на неравные углы:
∠ACH=∠B=3/5 *∠С, ∠BCH=2/5 *∠С
Биссектриса CD отстоит от стороны угла С на половину, следовательно проходит внутри того угла, который больше половины.
3/5 > 1/2