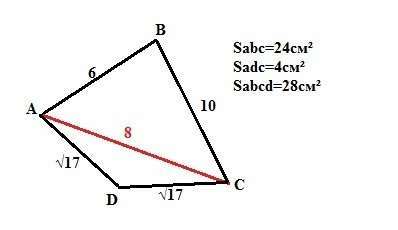
Четырехугольник делится диагональю АС на два треугольника со сторонами: АВ=6см, ВС=10см,АС=8см и AD=√17см, DC=√17см,АС=8см.
Площадь обоих треугольников можно найти по формуле Герона:
S=√(p(p-a)(p-b)(p-c), где р - полупериметр, a,b и c - стороны треугольника. Тогда
Sabc=√(12*6*4*2)=24cм²
Sadc=√((4+√17)*4*4*(√17-4))=4см²
Sabcd=Sabc+Sadc=24+4=28см².