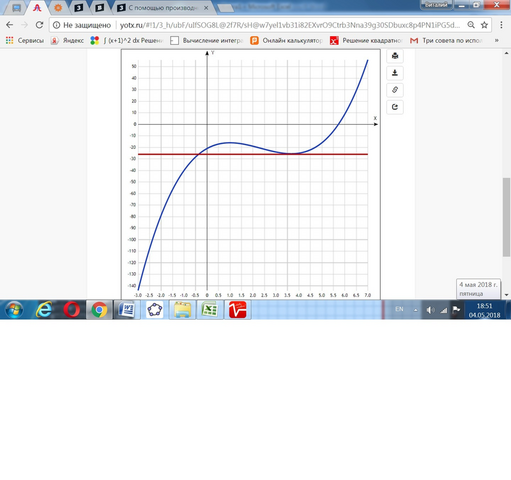
Дана функция F(x)= x^3-7x^2+11x-21.
1)Производная y' = 3х² - 14х + 11.
Приравняем её нулю:
3х² - 14х + 11 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-14)^2-4*3*11=196-4*3*11=196-12*11=196-132=64;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=√64-(-14))/(2*3)=(8-(-14))/(2*3)=(8+14)/(2*3)=22/(2*3)=22/6=11/3≈ 3.66667;x_2=(-√64-(-14))/(2*3)=(-8-(-14))/(2*3)=(-8+14)/(2*3)=6/(2*3)=6/6=1.
Найденные
точки выставляются на числовой прямой; к ним добавляются те точки, в которых
производная не определена. На промежутках находят знаки производной.
Где производная положительна - функция возрастает, где
отрицательна - там убывает.
Точки, в которых происходит смена знака и есть
точки экстремума - где производная с плюса меняется на минус - точка максимума,
а где с минуса на плюс - точки минимума.
Приводим таблицу значений производной.
х = 0 1 2
3,666667
4
у' = 11 0
-5
0 3.
Ответ: максимум в точке х = 1, минимум в точке х = 11/3.
2) Уравнение касательной у = y'(xo)(x - xo) + y(xo). xo = 1.
y'(xo) = 3*1² - 14*1 + 11 = 0,
y(xo) = 1³ -7*1² + 11*1 - 21 = -26.,Так как касательная в точке экстремума, то она горизонтальна.
Ответ: у = -26.