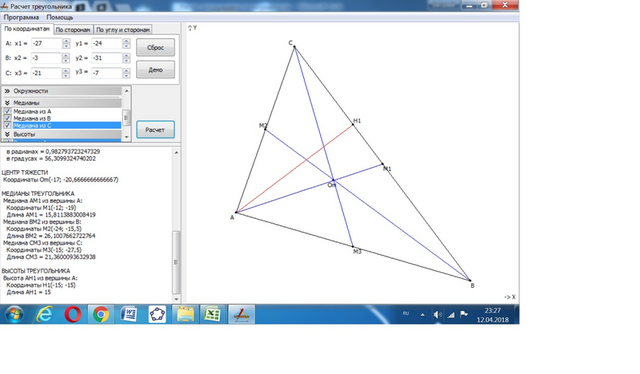
Даны координаты вершин треугольника АВС:
А(-27, -24) В(-3, -31) С (-21, -7).
Требуется:
1) вычислить длину стороны ВС = √((-21+3)²+(-7+31)²) = √900 = 30.
2) составить уравнение линии ВС:
(х+3)/(-18) = (у+31)/24.
4х +3у + 105 = 0.
у = (-4/3)х - 35.
3) составить уравнение высоты АН, проведенной из вершины А;
Угловой коэффициент АН = -1/к(ВС) = -1/(-4/3) = 3/4.
Получаем у = (3/4)х + в.
Для определения коэффициента в подставим координаты точки А:
-24 = (3/4)*(-27) + в.
Отсюда в = -24 + (81/4) = (-96 + 81)/4 = -15/4.
Уравнение высоты АН: у = (3/4)х - (15/4).
4) вычислить длину высоты, проведенной из вершины А;
Находим координаты точки Н как точки пересечения прямых ВС и АН.
(-4/3(х - 35 = (3/4)х - (15/4).
(-3/4)х - (4/3)х = 35 - (15/4),
(-25/12)х = 125/4,
х = (12*125)/(-25*4) = -15.
у = (-4/3)*(-15) - 35 = 20 - 35 = -15. Точка Н(-15; -15).
Длина АН = √((-15+27)²+(-15+24)²) = √(144+81) = √225 = 15.
5) найти точку пересечения медиан;
Эта точка К имеет средние координаты среди вершин.
К((-27-3-21)/3=-17; (-24-31-7)/3=-62/3) = (-17; (-62/3)).
6) вычислить внутренний угол при вершине В;
Расчет длин сторон.
АВ (с) =
√((Хв-Ха)²+(Ув-Уа)²)
= √625 =
25.
BC (а)=
√((Хc-Хв)²+(Ус-Ув)²)
= √900
= 30.
AC (в) =
√((Хc-Хa)²+(Ус-Уa)²)
= √325 ≈
18,02775638.
cos В= (АВ²+ВС²-АС²)/(2*АВ*ВС)
=
0,8.
B =
0,643501
радиан
=
36,8699
градусов.
7) найти координаты точки М, расположенной симметрично точке А относительно прямой ВС.
хМ = 2*хН - хА = 2*(-15) - (-27) = -30 + 27 = -3.
уМ = 2*уН - уА = 2*(-15) - (-24) = -30 + 24 = -6.