Помогите пожалуйста решитьзаранее спасибо

Question

Помогите пожалуйста решить
заранее спасибо

---

Answer 1

1) Все высоты в треугольнике пересекаются в одной точке, следовательно, если продлить СО, мы получим высоту СС1 с прямым углом АС1С. Получим прямоугольный треугольник АС1С, где известен угол ВАВ1=САВ=42 градуса. Тогда угол АСО=углу АСС1=90-42=48 градусов.
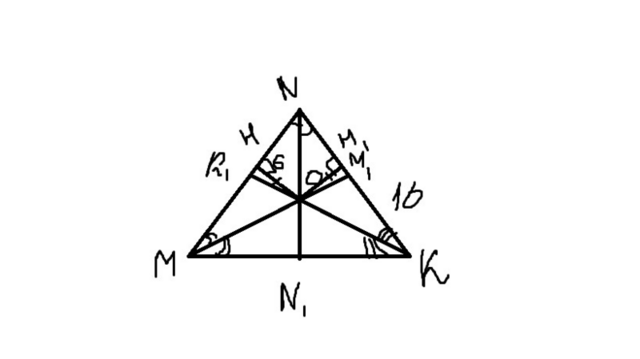
2) В треугольнике MNK MM1, NN1, KK1 - биссектрисы. Расстояние от стороны до точки О - это перпендикуляр ОН, а точка О по теореме о биссектрисах равноудалена от сторон треугольника. Следовательно, опустив перпендикуляр ОН1 к стороне NK, он также будет равен 6 см. Площадь треугольника равна половине произведения основания на высоту. NK=10 см по условию, ОН1 - высота треугольника(т.к.перпендикуляр к стороне), следовательно площадь=(6*10):2=30 см2

---

Comments

Извините, долго делала, не видела, что уже ответили. Может вам мой рисунок пригодится.

Answer 2

Вариант 1.
1. Проведём высоту СС1. Она пройдёт через точку О, потому что высоты треугольника пересекаются в одной точке О.В треугольнике АСС1 угол АС1С = 90 градусов, т.к. СС1 - высота, угол САВ = 42 градуса по условию. Угол АСС1 = 90 - 42 = 48 (градусов) - это и есть искомый угол АСО.Ответ: угол АСО = 48 градусов.
2. Т.к. точкой пересечения биссектрис является центр вписанной в треугольник окружности, то тогда расстояние от О до стороны MN = r. Тогда расстояние от О до стороны NK = MN = 6. S∆NOK = 1/2*6*10 = 30 см². Ответ: 30 см^2.