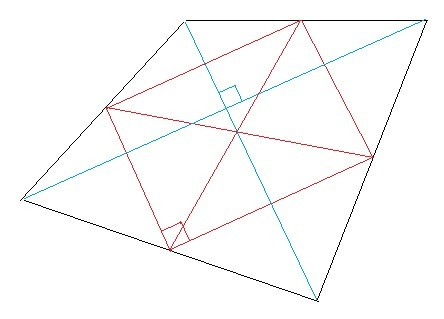
Середины сторон произвольного четырёхугольника являются вершинами параллелограмма (теорема Вариньона). Диагонали параллелограмма Вариньона равны, следовательно он является прямоугольником. Стороны параллелограмма Вариньона параллельны диагоналям данного четырехугольника, следовательно диагонали четырехугольника перпендикулярны.
S= 10*7*sin90 /2 = 35
-----------------------------------------------------------------------------------------------------------------
E,F,G,H - середины сторон произвольного четырехугольника. EFGH - параллелограмма Вариньона.
EF является средней линией в треугольнике ABC, EF||AC
GH является средней линией в треугольнике ADC, GH||AC
EH является средней линией в треугольнике BAD, EH||BD
FG является средней линией в треугольнике BCD, FG||BD