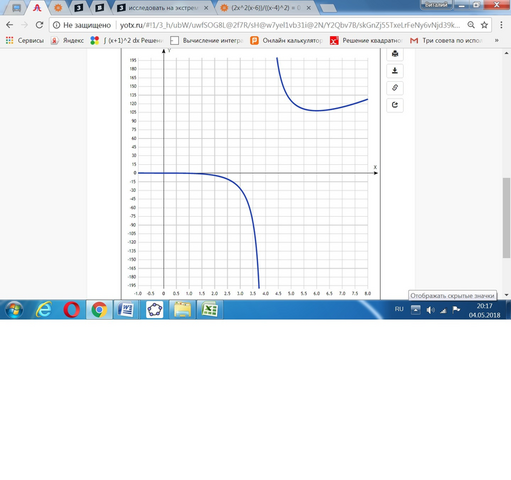
Дана функция y=x³/(x-4).
Её производная y' = (2x²(x - 6))/((x - 4)²).
Отсюда видно, что она равна нулю при х = 0 и х = 6.
Найденные
точки выставляются на числовой прямой; к ним добавляются те точки, в которых
производная не определена. На промежутках находят знаки производной.
Где производная положительна - функция возрастает, где
отрицательна - там убывает.
Точки, в которых происходит смена знака и есть
точки экстремума - где производная с плюса меняется на минус - точка максимума,
а где с минуса на плюс - точки минимума.
Находим знаки производной:
х = -1 0 1 6 7
у' =
-0,56
0
-1,11111
0
10,88889.
Как видим, критических точек две. а экстремум один - минимум в точке х = 6. у(6) = 108.
В точке х = 0 перегиб графика.