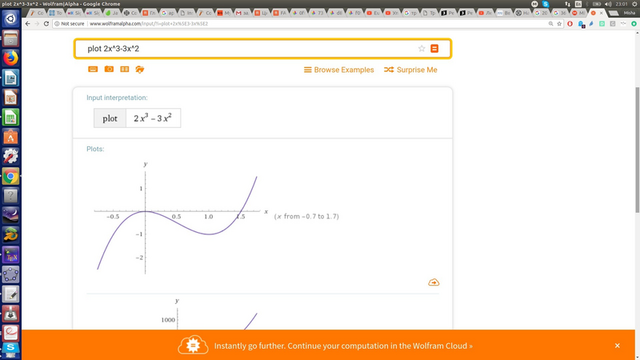
ищем критические точки:

смотрим, как ведет себя производная функции при переходе через эти точки:
![+++++++[0]---------[1]+++++++\ \textgreater \ x +++++++[0]---------[1]+++++++\ \textgreater \ x](https://tex.z-dn.net/?f=%2B%2B%2B%2B%2B%2B%2B%5B0%5D---------%5B1%5D%2B%2B%2B%2B%2B%2B%2B%5C+%5Ctextgreater+%5C+x)
производная в точке
0 меняет знак с
+ на
- , что означает, что точка

являеться максимумом функции

,
производная в точке 1 меняет знак с - на
+ , что означает, что точка

являеться минимумом функции

----------------
тогда промежутки монотонности:
ф-ия

монотонно растет на промежутке

ф-ия

монотонно убывает на промежутке

----------------
ф-ия

пересекает ось ОХ в точкаx


ф-ия

пересекает ось ОУ в точке

на основании этих данных и строиться схематический график