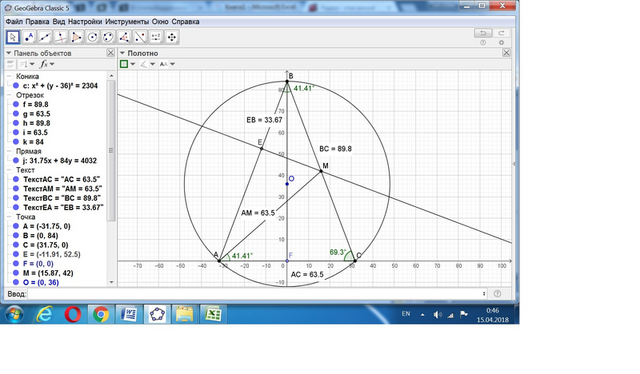
Из условия, что треугольники ABC и CAM подобны, вытекает равенство АМ и АС.
Используем формулу медианы:
ma = (1/2)*√(2b²+2c²-a²).
Для равнобедренного треугольника АВС стороны АВ (с) и ВС (а) равны а.
Получим с учетом АМ = АС = в:
b= (1/2)√(2b²+a²).
2b= √(2b²+a²) возведём в квадрат.
4b² = 2b²+a².
2b² = a².
b = a/√2.
Находим косинус угла С при основании треугольника.
cos C = (b/2)/a = a/)2√2*a) = 1/(2√2) = √2/4.
Для прямоугольного треугольника BCF cos C = sin(B/2).
Находим cos(B/2) = √(1 - sin²(B/2)) = √(1 - (2/16)) = √(7/8).
Тогда косинус угла В как двойного по отношению к (В/2) равен:
cos B = cos²(B/2) - sin²(B/2) = (7/8) - (2/16) = 6/8 = 3/4.
Теперь можно определить длину боковых сторон из треугольника ВМЕ, где его гипотенуза ВМ равна половине стороны ВС (а).
а = 2*ВЕ/(cos B) = 2*9√14/(3/4) = 24√14.
Основание АС (в) и медиана АМ равны а/√2 = 24√14/√2 = 24√7.
Высота BF равна:
BF = √(а² - (в/2)²) = √((24√14)² - (12√7)²) = √(
8064 -1008) = √7056 = 84.
Площадь S треугольника АВС равна:
S = (1/2)AC*BF = (1/2)*24√7*84 = 1008√7.
Отсюда находим искомый радиус описанной около треугольника АВС окружности:
R = a²b/(4S) = ((24√14)²*24√7)/(4*1008√7) = 8064/168 = 48.