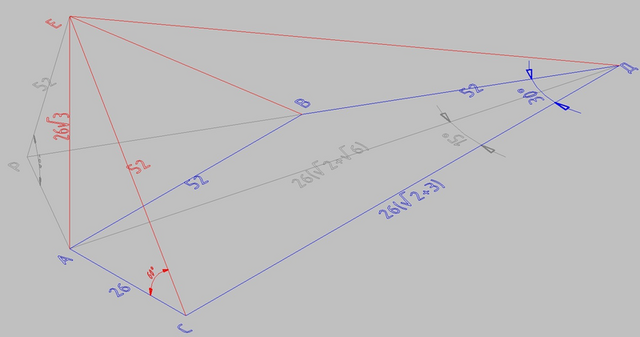
На картинке основание синее, боковые рёбра красные, вспомогательные построения серые
Из требования взаимной перпендикулярности боковых граней, содержащих короткое основание и короткую боковую сторону с основанием, вытекает, что трапеция прямоугольная, а
∠САЕ = ∠ВАЕ = 90°
Теперь площади.
--- 1 ---
ΔАСЕ
АС = 26 по условию
СЕ = 52 как гипотенуза в прямоугольном треугольнике с углом в 30°
АЕ = 26√3 (хоть по т. Пифагора, хоть через синус 60°)
S(ACE) = 1/2*26*26√3
S(ACE) = 2*13²√3
(13 не умножаем пока, дальше оно будет всплывать 100 раз)
--- 2 ---
ΔАСД
∠АСД = 15°
АД = АС/sin(15°) = 26(√2+√6)
(в конце с синусами возня отдельным пунктом)
АС/СД = tg(15°)
СД = АС/tg(15°) = 26(2+√3)
S(ECД) = 1/2*52*26(2+√3)
S(ECД) = 4*13²(2+√3)
--- 3 ---
ΔАРВ
АР = 26
т.к. ΔАРЕ и АСЕ имеют одну высоту АЕ, и одинаковый по условию угол
∠АРЕ = ∠АСЕ = 60°
∠АВР = 30° как угол с секущей ДВ при параллельных основаниях трапеции
АВ = 26*2 = 52 как гипотенуза ΔАВР против угла в 30°
S(АВЕ) = 1/2*52*26√3
S(АВЕ) = 4*13²√3
--- 4 ---
в ΔАВД
∠ВАД = ∠СДА = 15° (секущая при параллельных прямых)
∠ВДА = 15° как половина от угла в 30°
и ΔАВД - равнобедренный, ВД = АВ = 52
Теперь можем вычислить площадь ΔЕВД
S(EBД) = 1/2*ВД*ЕР = 1/2*52*52
S(EBД) = 8*13²
--- 5 ---
Боковая поверхность
S = 2*13²√3 + 4*13²(2+√3) + 4*13²√3 + 8*13²
S = 2*13²(√3 + 4 + 2√3 + 2√3 + 4)
S = 2*13²(8 + 5√3)
S = 2704 + 1690√3
--- 6 ---
ищем в поисковике таблицу синусов нестандартных углов, это π/12
нужен обратный синус 15°
sin (15°) = (√3 -1)/(2√2)
1/sin (15°) = 2√2/(√3 - 1)
Домножим числитель и знаменатель на (√3 + 1)
1/sin (15°) = 2√2*(√3 + 1)/(3 - 1) = √6 + √2
Ещё нужен котангенс, но он просто есть в табличке
1/tg(15°) = 2+√3