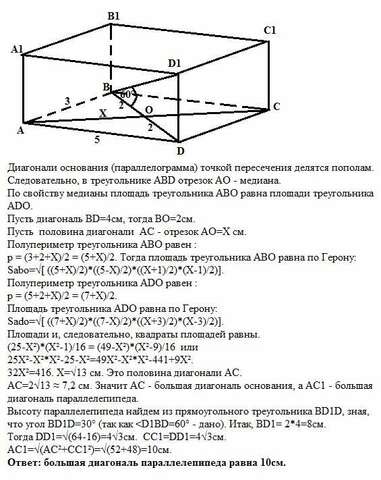
Диагонали основания нашего параллелепипеда (параллелограмма АВСD) точкой пересечения делятся пополам. Следовательно, в треугольнике АВD отрезок АО - медиана. По свойству медианы площадь треугольника АВО равна площади треугольника ADO.
Пусть диагональ BD=4см, тогда ВО=ОD=2см.
Пусть половина диагонали АС - отрезок АО=Х см.
Полупериметр треугольника АВО равен :
р = (3+2+Х)/2 = (5+Х)/2. Тогда площадь треугольника АВО равна по Герону:
Sabo=√[ ((5+Х)/2)*((5-Х)/2)*((Х+1)/2)*(Х-1)/2)].
Полупериметр треугольника АDО равен :
р = (5+2+Х)/2 = (7+Х)/2.
Площадь треугольника АDО равна по Герону:
Sado=√[ ((7+Х)/2)*((7-Х)/2)*((Х+3)/2)*(Х-3)/2)].
Площади и, следовательно, квадраты этих площадей равны.
(25-Х²)*(Х²-1)/16 = (49-Х²)*(Х²-9)/16 или
25Х²-Х²*Х²-25-Х²=49Х²-Х²*Х²-441+9Х².
32Х²=416. Х=√13 см. Это половина диагонали АС.
АС=2√13 ≈ 7,2 см. Значит АС - большая диагональ основания, а АС1 - большая диагональ параллелепипеда.
Высоту параллелепипеда найдем из прямоугольного треугольника BD1D, зная, что угол BD1D=30° (так как Итак, ВD1= 2*4=8см.
Тогда DD1=√(64-16)=4√3см. СС1=DD1=4√3см.
AC1=√(АС²+СС1²)=√(52+48)=10см.
Ответ: большая диагональ параллелепипеда равна 10см.