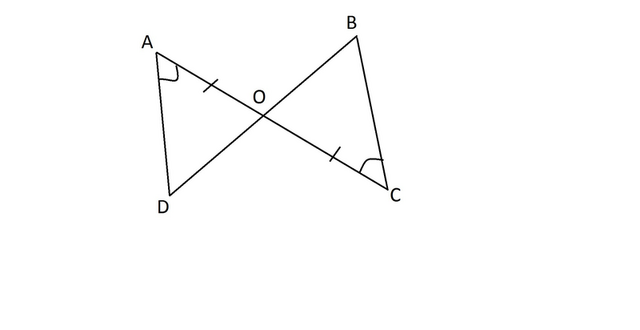
Чертеж приклепляю, он примерный.
Прежде всего, углы AOD и BOC вертикальные, а значит равны.
BCO=DOC, AOD=BOC, АО=ОС(т.к О- середина отрезка) значит треугольники BOA и DOC равны по второму признаку равенства треугольников(по 2 углам и прилежащей стороне)
Один вопрос, что геометрия 7 класса забыла в начальных классах?