В окружности провдены две взаимно перпендикулярные хорды. одна из хорд удалена от центра...

Question

В окружности провдены две взаимно перпендикулярные хорды. одна из хорд удалена от центра на расстояние 6, другая - на расстояние 8. на каком расстоянии от центра окружности находится точка пересечения хорд?

Answer 1

Если провести растояния от центра к хордам то получим прямоугольник со сторонами 6 и 8.

Проведем диагональ  которая имеетвершины в точках пересечения хорд и центре окружности.

По теореме обратной теореме пифагора сумма квадратов катета равна кварату гипотенузы a^2+b^2=c^2

Значит растояние от центра до точки пересечения равна 10 см

Answer 2

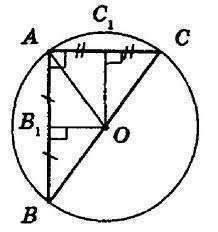
!!! Работаем по рисунку:

1)АС перпендикуларна АВ ( по условию), А - точка пересечения хорд.

2)ОВ1=6, ОС1=8, ОА-?    АВОС1- прямоугольник, ОА- диагональ.

   Из Δ АОВ1-прям.: ОА= √ОВ1²+ОС1²=√6²+8²=√100=10

Это справедливо и на тот случай, если точка пересечения хорд находится внутри окр-сти.

Ответ:10. 

---