В круг вписан квадрат со стороной 9√2 см, найти сторону правильно треугольника,...

Question

В круг вписан квадрат со стороной 9√2 см, найти сторону правильно треугольника, описанного вокруг этого круга

Answer 1

Ищем диаметр окружности.

Радиус, следовательно, 9.

Радиус окружности вписанной в правильный треугольник находится по формуле 
Итого:

Answer 2

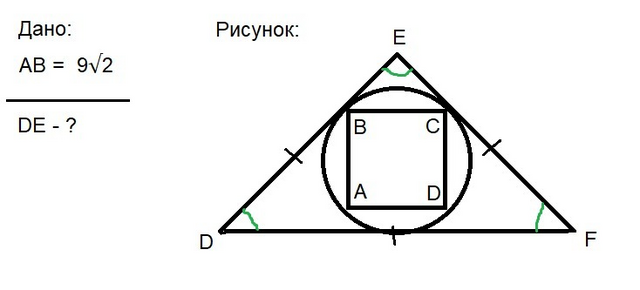
1. Рассмотрим квадрат ABCD.
    Диагональ квадрата равна радиусу окружности. Следовательно, 
    диагональ квадрата вычисляется по формуле:
    c = a · √2, ⇒
    9√2 · √2 = 18.
    Найдём радиус окружности: r = 18 ÷ 2 = 9

2. Рассмотрим ΔDEF
    ΔDEF - правильный (по усл.) и описан около окружности, ⇒
    его сторона вычисляется по формуле:
    a = r · 2√3, ⇒
    9 · 2√3 = 18√3

Ответ: 18√3

---

Comments

Решение выше верное, в отличие от моего.

---

Треугольник не описан, а вписан в окружность.

---

* находится внутри окружности