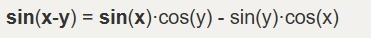Sin(x-60)=cos(x+30)
Раскроем обе части уравнения по формулам (формулы для раскрытия на картинке):
Sin(x-60)=sin(x)*cos(60)-cos(x)*sin(60)
cos(x+30)=cos(x)*cos(30)-sin(x)*sin(30)
Перенесем все части уравнения на одну сторону:
sin(x)*cos(60)-cos(x)*sin(60)-cos(x)*cos(30)+sin(x)*sin(30)=0
(sin(x)*cos(60)+sin(x)*sin(30))-(cos(x)*sin(60)+cos(x)*cos(30))=0
sin(x)*(cos(60)+sin(30))-(cos(x)*(sin(60)+cos(30))=0
sin(x)*2*cos(60)-(cos(x)*2*cos(30))=0
sin(x)-cos(x)*√3=0
sin(x)=cos(x)*√3
sin(x)=√(1-sin²(x))*√3
sin(x)=√(3-3*sin²(x))
3-3*sin²(x)=sin²(x)
3-(3*sin²(x)+sin²(x))=0
3-4*sin²(x)=0
4*sin²(x)=0
sin(x)=0
x=0