В треугольнике ABC угол С равен 90 , CH - высота , BC=12 , BH=6. Найдите sin A

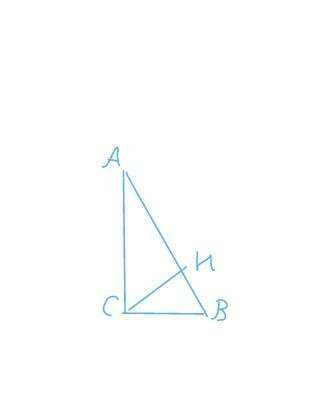
1) ∆ВСН, <ВНС=90°. $\frac{bh}{bc} = \frac{6}{12} = \frac{1}{2}$
ВН=½ВС, поэтому <ВСН, лежащий напротив катета ВН, равен 30° 
2) <С=<ВСН+<АСН=90° <АСН=90°-<ВСН=90°-30°=60° 
3) Сумма острых углов прямоугольного треугольника равна 90°
∆АСН, <АНС=90° <А=90°-<АСН=90°-60°=30° 
4) sinA=sin30°=½

Отвт: ½