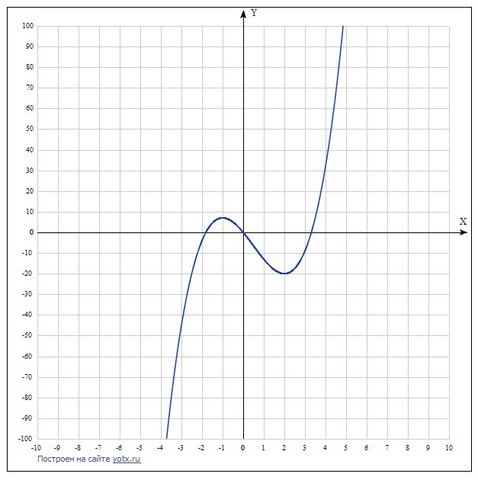
Исследовать на выпуклость функцию
y(x)=2x³ -3x² - 12x
Решение Находим первую производную функции
y' = (2x³ -3x² - 12x)' = (2x³)' -(3x²)' - (12x)' = 6x² - 6x - 12
Находим вторую производную функции
y" =(
6x² - 6x - 1)' = (6x²)' - (6x)' - 12' = 12x - 6
Находим критические точки приравняв вторую производную к нулю y" = 0 ⇔ 12x - 6 = 0
x = 0,5 Отобразим на числовой прямой эту точку и найдем знаки второй производной по методу подстановки. Например при х=0 12х-6 = -6<0 <br> - 0 +
------------------!----------------- 0,5
Вторая производная отрицательна и функция выпукла вверх
при x∈(-∞ ; 0,5);
Вторая производная положительна и функция вогнута(выпукла) вниз
при x∈(0,5 ; +∞).
В точке х=0,5 y=-6,5 функция имеет точку перегиба. График функции во вложении