Помогите решить спасибо!

Question

Дан 1 ответ

Gromoff97_zn · Answer 1 · 2018-08-05T08:32:40+0000

$log_7 (49*x^2 - 25) - log_7 x \leq log_7 (50*x - \frac{9}{x} + 10)$
Сразу за ОДЗ :
1) из-за дроби $\frac{9}{x}$ у нас $x \neq 0$ (но потом это всё равно "выколится")
2) $49*x^2 - 25 \ \textgreater \ 0$
$(7x-5)(7x+5) \ \textgreater \ 0$
а отсюда
$x \in (-\infty;-\frac{5}{7}) \cup (\frac{5}{7};\infty)$
3)

0" alt="50*x - \frac{9}{x} + 10 > 0" align="absmiddle" class="latex-formula">
Это эквивалентно следующему:
$\frac{50*x^2 + 10*x - 9}{x} \ \textgreater \ 0$
Найдя корни квадратного уравнения в числителе, решаем это неравенство методом интервалов (внизу будет уже 1 пример с рисунком, так что второй раз уже не буду делать, а лишь укажу промежуток) и получаем :
$x \in (\frac{-1 - \sqrt{19}}{10};0) \cup (\frac{-1+\sqrt{19}}{10};\infty)$

При пересчении итоговое ОДЗ будет очень простым :
$x \in (\frac{5}{7};\infty)$

Решаем неравенство :
$log_7 (49*x^2 - 25) \leq log_7 (50*x - \frac{9}{x} + 10) + log_7 (x)$
$log_7 (49*x^2 - 25) \leq log_7 (50*x^2 + 10*x - 9)$
$49*x^2 - 25 \leq 50*x^2 + 10*x - 9$
$- 25 \leq x^2 + 10*x - 9$
$0 \leq x^2 + 10*x + 16$
$x^2 + 10*x + 16 \geq 0$
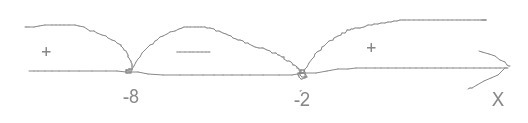
Далее находим корни уравнения (-8 и -2) и преобразовываем неравенство :
$(x+8)(x+2) \geq 0$
рисуете интервалы (см. рисунок), и получается, что без ОДЗ
$x \in (-\infty;-8] \cup [-2;\infty)$
Пересечём это с нашим ОДЗ, и получим тот же промежуток, что и в ОДЗ:
$x \in (\frac{5}{7};\infty)$
Ответ : $x \in (\frac{5}{7};\infty)$