Перепишем уравнения в цилиндрической системе координат: (x, y, z) меняются на (r, φ, z) по формулам x = r cos(φ - arctg 3/4), y = r sin(φ - arctg 3/4) – арктангенс возник из соображений удобства, чтобы третье уравнение выглядело поприличнее. Откуда отсчитывать углы, для нас не принципиально.
Первое уравнение:

Второе уравнение не меняется.
Третье уравнение:

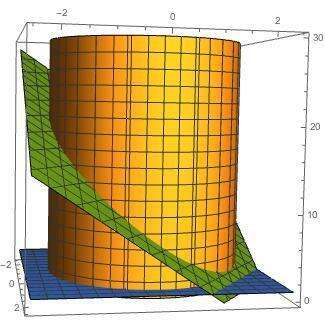
Итак, уравнения поверхностей, ограничивающих тело, выписаны выше: r = 2, z = 1, z = 12 - 5r sin φ. Тело, которое они ограничивают, изображено на приложенном рисунке: это часть цилиндра, вырезанная двумя плоскостями.
Сформулируем условия в виде неравенств.
1 ≤ z ≤ 12 - 5r sin φ
0 ≤ φ ≤ 2π
0 ≤ r ≤ 2
Осталось вспомнить, что элемент объёма в цилиндрических координатах есть dV = r dr dφ dz, и вычислить интеграл:

Ответ: 44π.
________________________________________
Для самопроверки получим этот ответ без интеграла.
Самая нижняя точка, в которой наклонная плоскость пересекает цилиндр, это z = 12 - 5 * 2 = 2, самая высокая – z = 12 + 5 * 2 = 22. Тогда объём равен сумме объёма цилиндра с высотой 2 - 1 = 1 и половины объёма цилиндра с высотой 22 - 2 = 20.
V = S * (h1 + h2 / 2) = 4π * (1 + 10) = 44π