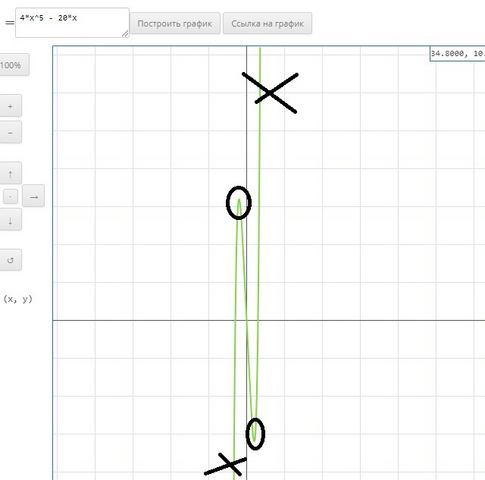
Сначала продифференцируем;
Y' = 20 * x^4 - 20;
Найдём значения икса, при которых производная равна 0.
Y' = 20 * x^4 - 20 = 0;
20 * x^4 = 20;
x^4 = 1;
x = плюс и минус единица.
При этих значениях икс производная функция равна нулю, что значит, что сама функция при этих икс терпит пик значения.
При икс = 1, Y = -16; Подставляем икс в исходную функцию.
При икс = -1, Y = 16; Подставляем икс в исходную функцию.
Таким образом наибольшее значение функции будет при икс равном -1 на отрезке [-1;1]