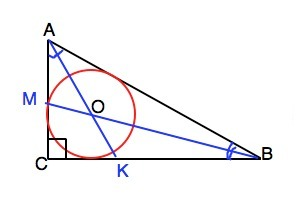
Найдите величину угла АОВ, где АВ - гипотенуза прямоугольного треугольника, а О - центр вписанной в треугольник окружности.
------------
Центр вписанной в любой треугольник окружности находится на пересечении биссектрис его углов.
Т.к. АВ - гипотенуза, больший угол С=90° как лежащий против большей стороны.
Пусть АК и ВМ - биссектрисы углов А и В соотсетственно. Тогда точка их пересечения О - центр вписанной окружности.
Сумма острых углов прямоугольного треугольника 90°, поэтому сумма их половин - 45°. В ∆ АОВ (угол ОАВ+ угол АВО):2=45°. Из суммы углов треугольника
угол АОВ=180°-45°=135°