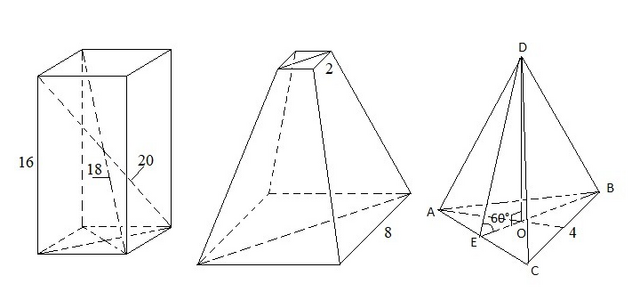
1) Найдём диагонали основания по Пифагору.
D = √(20² - 16²) = √(400 – 256) = √144 =
12
d
= √(18² - 16²) = √(324 – 256) = √68
a = √(D +d)/2
a
= √(12² + (√68)²)/2 = √(144 + 68)/2 =√212/2 = √53
Ответ: √53
дм.
2) Основания
– квадраты. D –
диагональ большего основания, d
– диагональ меньшего основания.
Диагональное сечение – трапеция высотой 4 и с основаниями D и d.
D =
8√2; d = 2√2
S =
1/2*(8√2 + 2√2)*4 = 1/2* 10√2* 4 = 20√2
Ответ: 20√2
дм².
3) ABC – равносторонний треугольник, EO – радиус вписанной окружности, r = a√3/6.
EO =
4√3/6 = 2√3/3
DE – апофема, ∠EDO = 90 – 60 = 30°
⟹ DE = 2EO = 4√3/3
DO – высота пирамиды, DO = √(DE² - EO²)
DO = √((4√3/3)² - (2√3/3)²) = √(16*3/9 – 4*3/9) = √(48/9 – 12/9) = √(36/9) = √4 = 2
V = ha²/4√3
V = 2*4²/4√3 = 2*16/4√3 = 8/√3 = 8√3/3
Sосн. = √3/4 * a²; Sбок. = 1/2PL
S осн. = 4²*√3/4 = 16√3/4 = 4√3; Sбок. = 1/2*16*4√3/3 = 32√3/3
S = 4√3 + 32√3/3 = 12√3/3 + 32√3/3 = 48√3/3 = 16√3
Ответ: V
= 8√3/3 см³, S = 16√3 см².